Вторая глава диссертации Шумкова Евгения
Александровича «Система поддержки принятия решений предприятия на основе
нейросетевых технологий».
Совместная разработка Шумкова Е.А. и Стасевича В.П.
Защищено патентом на изобретение РФ №20031338197/09(041224)
«Интеллектуальный контроллер с нейронной сетью и
правилами самомодификации». ФИПС 2005.
Глава 2. Топология «Внутренний
учитель»
Задача построения системы
управления сложным объектом или комплексом объектов в недетерминированной среде
нетривиальна. Как правило, синтез системы управления производится с
использованием известных технических решений, которые с минимумом переработок
внедряются в новой предметной области. В ряде случаев, готовых решений оказывается
недостаточно. Тем не менее, во всех случаях разработка системы управления
предполагает анализ условий функционирования системы, на базе которого
производится синтез модели. Распространены способы построения систем на основе:
конечно-автоматных моделей [3,15,27,31,46,48], сетей Петри [27,79], генетических алгоритмов [84,95], аппарата нечеткой логики [5, ,13,43,58,77,80,81], нейронных сетей [28,29,137,136,144,187,160,184] и др. Также в последнее время стали появляться
системы на основе теории хаоса [102]. Наиболее распространенный подход основан на
использовании механизма целевой функции, включающего экстремальные методы
проектирования. Однако такой подход не всегда позволяет построить адаптивную
систему управления. В частности, такие примером являются системы, действующие в
недетерминированной среде. Поэтому мы посчитали целесообразным разработать свой
подход к построению таких систем.
Одним из существенных
недостатков известных методов проектирования систем управления сложными
объектами является отсутствие системного подхода. Во многих случаях система
строится из разрозненных функциональных блоков, что не позволяет в полной мере
оценить ее работоспособность и эффективность. Более того, часто и вовсе непонятно
как она будет работать в целом, и только испытания системы подтверждают (или не
подтверждают) ее работоспособность.
Итак, в данной главе
описывается наша методология построения систем управления сложными объектами в
недетерминированной среде.
Введем ряд определений:
·
недетерминированная
среда – среда, воздействие которой трудно описать статистическими методами;
·
адаптивная
система управления – система управления, позволяющая объекту изменять своё
поведения в зависимости от изменения характера внешних влияющих факторов;
·
целевая
функция – система управления должна работать таким образом, чтобы подкрепление
не убывало с течением времени и, если возможно, увеличивалось;
·
качество
работы системы – сравнение реального управления и целевой функции.
В рамках данной
терминологии приведем некоторые примеры систем управления комплексом объектов в
недетерминированной среде. К таким задачам относятся, например:
·
комплекс
светофоров на сложных перекрестках (транспортные потоки не поддаются
статистическому анализу);
·
мобильные
роботы-грузчики (здесь недетерминированным является порядок поступления
запросов на определенные грузы или товары);
·
комплекс
лифтов в многоэтажном здании (пассажиропоток постоянно изменяется, в случае,
скажем, переносов мероприятий с одного этажа на другой, поток пассажиров с
этого этажа увеличится, и предсказать это нет возможности);
·
прогнозирование
финансовых показателей (финансовые потоки поддаются статистическому анализу, но
результат низкий).
Указанные системы имеют
различную природу и среды функционирования, но способы организации управления,
а также методы построения нередко схожи.
Перейдем к предпосылкам,
заставившим нас разработать свой метод построения систем управления.
В рамках системного
подхода необходимо не только рассматривать систему как функциональное целое, но
и рассматривать все возможные процессы в системе, как часть одного большого
общего процесса управления. Обучение системы не должно быть отдельным и
независимым действием, оно должно органически вписываться в общую схему
взаимодействия системы и среды. В рассмотрении вопросов обучения и
функционирования системы неотъемлемо друг от друга и есть системность подхода.
Процесс управления и обучения рассматривается нами как единый процесс «жизни»
системы. В этом смысле предлагается, что всякую сложную управляющую систему
нужно рассматривать как адаптивную, как единую в смысле управления и обучения.
В частности, подход,
когда система проектируется так, что обучение проходит у разработчиков, являет
собой пример несистемного подхода к проектированию. Система изначально
построена раздробленно. Единожды обучившись, система управления функционирует
потом только в виде контура простейшего управления не модифицируясь.
Известны различные
подходы к обучению адаптивных систем управления. Традиционные методы обучения
предполагают использование баз знаний и правил.
Обычно, база правил не изменяется в процессе управления, в то время как
поведение среды может потребовать их изменений. Кроме того, часто сложно
формализовать правила, что тоже, в конечном счете, ведет к недостаточной
эффективности системы управления в целом.
Обучение с учителем
позволяет только один лишь раз обучить систему у разработчика, либо необходимо
наличие специалиста у себя. Здесь видно отсутствие системного подхода, о
котором мы говорили выше. Мы выберем для себя комбинированное обучение,
поскольку система должна дообучаться в процессе функционирования. В качестве
аппарата для построения системы, выберем нейронные сети, как наиболее удобные
для реализации нашей структуры. При этом будем использовать принципы обучения с
подкреплением и методики SMP. Существует множество примеров построения систем с использование
нейронных сетей в топологии с подкреплением. Наиболее близкие нам – сети
адаптивной критики. Однако они не подходят нам по ряду причин.
Итак, сформулируем
задачи, стоящие перед нами, как разработчиками самообучаемой системы
управления:
·
объект
или комплекс объектов в недетерминированной среде должен выполнять определенную
задачу, причем выполнять с заданными показателями качества;
·
при
выполнении задачи на основании информации от внешней среды объект, при
необходимости, изменяет свое поведение (изменяется тактика, при этом объект не
дообучается);
·
объект
должен обучаться на своих ошибках, путем выявления изменившегося характера
воздействия среды (изменяется стратегия, – объект должен выработать новые способы
реакции на воздействия).
Следовательно, для
решения указанной задачи необходимо разработать такую структуру системы и такой
метод обучения, которые реализуют идею обучения
самообучению. Система управления должна обучаться учителем не конкретным
реакциям на конкретные воздействия, а способу самообучения новым ситуациям. Назовем топологию такой нейросети топологией
«внутренний учитель», а метод обучения назовем «обучение самообучению».
При этом нужно сказать,
что вновь разработанная топология и метод обучения, суть две стороны одного и
того же принципа построения системы – принципа обучаемой самообучению системы.
С точки зрения
эпистемологии данной идее обучения самообучению ближе теория Пиаже [164]. То есть в своей работе мы предполагаем, что
познание есть биологическая функция. Нас интересует поиск механизмов
биологической адаптации. Мысль о том, что процесс приобретения знаний
адаптивен, еще конце 19-го века предложена Джеймсом, Зиммелем и другими, однако
Пиаже первым заметил, что адаптация в когнитивной (концептуальной) плоскости
совсем не то же самое, что физиологическая адаптация биологического организма.
Знание возникает в результате активной деятельности субъекта, будь она
физической или ментальной. Главное, что придает знанию организованность – это
целенаправленный характер данной деятельности. Любое знание привязано к
действию – знать объект или событие означает использование его в той или иной
деятельности.
Рассмотрим структуру предлагаемой
системы. Система состоит из нескольких структурных компонент. Схема
взаимодействия компонент представлена на рисунке 7. Основная компонента системы
– решающая нейросеть («решатель»). Она получает на вход сведения о текущем
состоянии среды и объекта. Входы этой нейросети формируются сенсорной
компонентой («сенсоры»). Выходы обрабатываются моторной компонентой
(«моторика»). Важнейшая часть системы – компонента обучения («учитель»). Именно
здесь оценивается состояние среды с точки зрения изменения тактики и стратегии поведения,
а также формируются измененные правила поведения системы. На вход этой
компоненты подаются сведения о подкреплении.
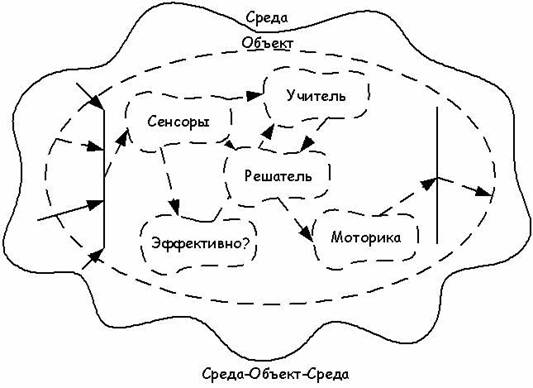
Рисунок 7 - Структура взаимодействия компонент
Для определения своих
ошибок система должна знать, насколько эффективно она работает в данный момент.
В качестве подкрепления в систему введен коэффициент эффективности. Этот коэффициент
эффективности используется для выявления изменения стратегии и тактики поведения
улучшившего или ухудшившего общую оценку работы. Такой коэффициент является
основным источником информации для построения эффективной схемы самообучения.
При этом коэффициент должен вычисляться на основе обработки сведений о внешней
среде, объекте, и о характере взаимодействия объекта со средой. С точки зрения
системного анализа это показатель эффективности.
Коэффициент эффективности
вычисляется в отдельной компоненте – блок коэффициента эффективности (БКЭ) и
управляет процессом самообучения. Только благодаря этому коэффициенту система
управления понимает в какую сторону изменилась ее стратегия и тактика – в
лучшую или в худшую.
Процесс обучения системы
заключается в запоминании эталонных реакций на воздействия. За счет
использования нейронных сетей обучение может проводиться с опережением на
основе прогноза, с последующей корректировкой. Это свойство используется с той
целью, что необходимо быть готовым к незнакомым воздействиям (примерам) и
адекватно на них реагировать.
Процесс самообучения
заключается в формировании компонентой обучения дополнительных данных об эталонных
реакциях на определенные воздействия и дообучения (или переобучения, в
зависимости от выбранного алгоритма обучения нейронной сети) решающей
компоненты. При этом выбор дополнительных данных производится на базе
информации от компоненты обратной связи, а сами дополнительные данные поступают
с сенсорной компоненты.
Задача сенсорной компоненты предоставить
информацию о внешней среде и объекте компоненте обучения, решающей компоненте и
компоненте вычисления коэффициента эффективности. Задача моторной компоненты –
реализовать управляющие воздействия. Центральный узел топологии в структурном
виде представлен на рисунке 8.
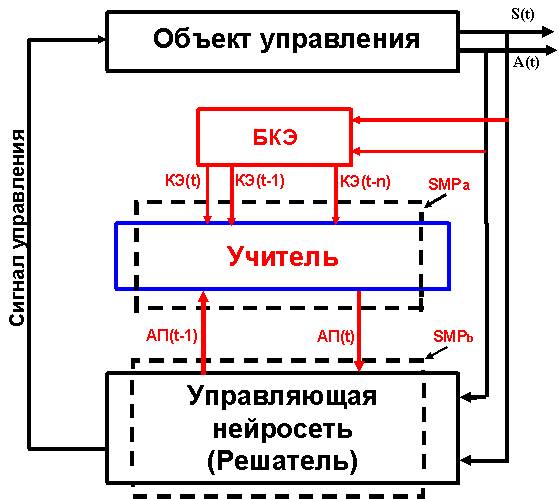
Рисунок 8 - Центральный узел топологии «внутренний учитель»
Введем следующие
обозначения:
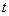 - время (цикл управления);
- время (цикл управления);
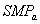 - правила самообучения компоненты учителя;
- правила самообучения компоненты учителя;
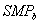 - правила управления компоненты решателя;
- правила управления компоненты решателя;
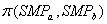 - общая политика самообучения объекта;
- общая политика самообучения объекта;
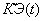 - коэффициент эффективности на итерации
- коэффициент эффективности на итерации 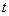 ;
;
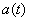 - действие объекта на цикле управления
- действие объекта на цикле управления 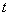 , где
, где 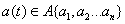 ;
;
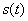 - состояние объекта на цикле управления
- состояние объекта на цикле управления 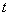 , где
, где 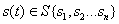 ;
;
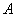 - пространство действий объекта;
- пространство действий объекта;
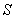 - пространство состояний объекта;
- пространство состояний объекта;
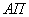 - адаптационный параметр;
- адаптационный параметр;
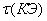 - глубина временного погружения по
- глубина временного погружения по 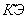 ;
;
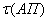 - глубина временного погружения по АП (последний цикл
управления не учитывается);
- глубина временного погружения по АП (последний цикл
управления не учитывается);
Также введем несколько
определений относящихся к времени:
Итерация - законченный цикл управления объектом, т. е. цикл между воздействием
внешней среды и реакцией системы управления на него.
Критическое время 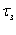 – время установленное разработчиком, за
которое система обязательно должна восстановить заданный коэффициент эффективности,
в противном случае система не отрабатывает задание.
– время установленное разработчиком, за
которое система обязательно должна восстановить заданный коэффициент эффективности,
в противном случае система не отрабатывает задание.
Период дообучения 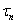 – время, за которое система при потере
заданного значения коэффициента эффективности, вновь должна на него выйти.
Определяется как
– время, за которое система при потере
заданного значения коэффициента эффективности, вновь должна на него выйти.
Определяется как
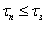 (2.1)
(2.1)
Сенсоры
– это компонента получения информации от среды. Посредством сенсоров система
считывает информацию о состоянии среды и о состоянии объекта. На базе этих
сведений принимается решение об управлении, подсчитывается коэффициент
эффективности.
Сенсоры
могут реализоваться как на базе нейронных сетей, так и на традиционных
алгоритмах, так как в этой компоненте реализуются простейшие функциональные
зависимости. Вообще говоря, какие будут использоваться сенсоры или что под ними
будет пониматься – зависит от задачи.
В качестве решателя может
быть нейронная сеть. Тип и метод обучения зависят от решаемой задачи. Цель решателя –
получить входной вектор, пропустить его через себя и выдать результат. На
рисунке 9 показан решатель на основе послойно - полносвязной нейронной сети
прямого распространения.
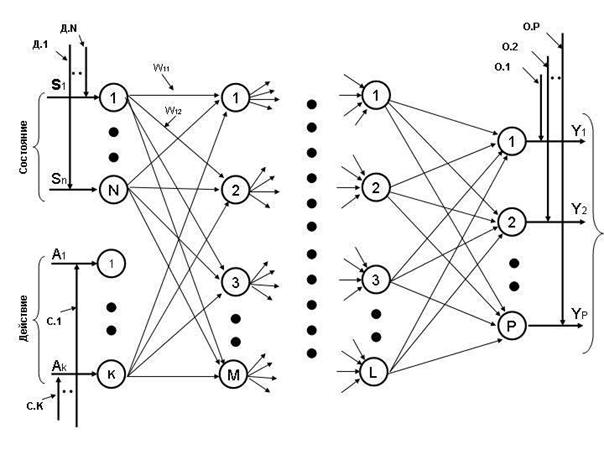
Рисунок 9 - Решатель в
разрезе нейронов
Первоначальные
правила управления формируются разработчиком. Правила должны формироваться с учетом того, что при
взаимодействии компонент и самообучении системы, они могут изменяться. Учитель,
изменяя правила управления, дообучает (переобучает) систему. Структура
взаимодействия и принцип дообучения (переобучения) в каждом конкретном случае
может быть индивидуальна, но можно выделить общие моменты (они будут
рассмотрены ниже).
Следует
отметить следующее, заложенное в систему свойство – решатель может работать как
в связке с учителем, так и отдельно, что очень удобно при программной
реализации. В случае вступления в процесс обучения учителя активируются входы
Д.1 – Д.N, C.1 – С.K
и выходы О.1 – О.P. В это
время входы 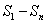 и
и 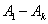 ,
которые подаются с сенсоров, равны нулю. После обучения, наоборот активируются
входы
,
которые подаются с сенсоров, равны нулю. После обучения, наоборот активируются
входы 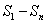 и
и 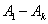 .
.
Начальную
инициализацию нейронной сети решателя можно производить стандартным образом, т.
е. за счет генератора случайных чисел, а можно и с помощью специальных методов
использующих знания о функционировании системы, например FBANN [18].
Внутренним устройством учителя
может быть послойно - полносвязная нейронная сеть прямого распространения, с
одним скрытым слоем (хотя не исключены случаи, когда может потребоваться
несколько скрытых слоев). Входы учителя – изменение коэффициента эффективности
за последний период времени (или за несколько последних), плюс адаптационные параметры
(один или несколько) за предыдущий период времени. Выход учителя показывает,
как изменить правила управления (рисунок 10).
В данной компоненте оценивается
состояние среды с точки зрения изменения тактики и стратегии поведения, и здесь
формируются измененные правила поведения системы.
Учитель реализует
политику самообучения 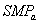 . Для
реализации принципа обучения самообучению введем общий вид функций вычисляющих
АП и КЭ:
. Для
реализации принципа обучения самообучению введем общий вид функций вычисляющих
АП и КЭ:
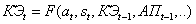 (2.2)
(2.2)
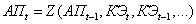 (2.3)
(2.3)
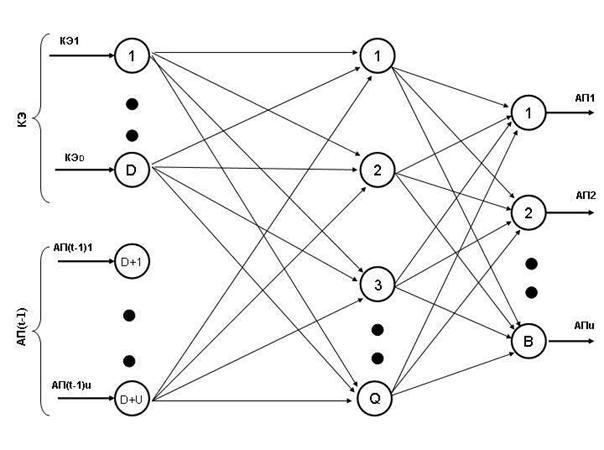
Рисунок 10
- Учитель в разрезе нейронов
Отметим, что 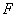 не является функцией обратной
не является функцией обратной 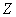 и
наоборот. Т. е. получается декомпозиция функций. Таким образом, политики
и
наоборот. Т. е. получается декомпозиция функций. Таким образом, политики 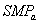 и
и 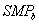 зависят от
зависят от 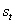 ,
, 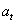 ,
, 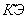 , АП и,
возможно других параметров.
, АП и,
возможно других параметров.
Учителя необходимо
обучить на правилах (2.8 – 2.34), то есть аппроксимировать правила нейронной
сетью.
Также необходимы еще два правила не входящих в
выборку обучения нейросети учителя:
MR1. Сброс всех настроек;
MR2. Обмен параметрами обучения и
настройками.
Правило MR1 применяется в случае, если время
обучения превышает критическое (предел задается разработчиком).
Правило MR2 применяется в случае, если имеется
несколько однотипных объектов управления и 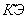 одного объекта значительно меньше, чем у
других и в этом случае происходит передача параметров от одного объекта к
другому.
одного объекта значительно меньше, чем у
других и в этом случае происходит передача параметров от одного объекта к
другому.
В общем случае количество
правил самообучения учителя определяется по формуле:
 (2.4)
(2.4)
Введение в топологию
учителя сокращает время обучения нейронной сети (численные характеристики в
главе 4), а также повышает адаптационные свойства объекта управления.
Также отметим возможность
создания учителя, который вычисляет необходимую скорость изменения параметров
адаптации, как показано на рисунке 11.
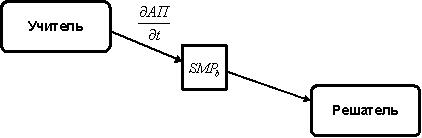
Рисунок 11 - Обучение по скорости изменения АП
В данном случае правила
самообучения решателя 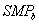 зависят главным образом от
зависят главным образом от 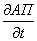 .
.
Нейросеть учителя
обучается при первом запуске системы.
Блок
коэффициента эффективности хранит историю изменения коэффициента эффективности.
В истории сохраняется определенное количество последних значений коэффициента,
которые получила система управления. На базе этой истории вычисляется
коэффициент эффективности за один или несколько одинаковых по продолжительности
периода времени. Это необходимо для вычисления динамики изменения коэффициента
эффективности. На каждом из нескольких периодов вычисляются средние величины коэффициента
эффективности, и сравниваются для соседних периодов. Причем для каждой динамики
могут быть 3 значения:
·
коэффициент эффективности снизился;
·
коэффициент эффективности вырос;
·
коэффициент эффективности не изменился.
Далее
эти показателя поступают на вход учителя, который, согласно правилам
самообучения, определяет, необходима ли модификация правил управления и
модифицирует их в случае необходимости.
Длина
истории, а также параметры подсчета среднего КЭ должны быть модифицируемыми, и
подстраиваться в зависимости от среды и объекта.
Для подсчета коэффициента
эффективности предлагается использовать шаблон:
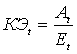 (2.5),
(2.5),
где 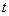 – период времени, для которого вычисляем коэффициент
эффективности;
– период времени, для которого вычисляем коэффициент
эффективности;
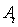 - безразмерный показатель полезной
деятельности, произведенной системой;
- безразмерный показатель полезной
деятельности, произведенной системой;
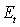 - безразмерный показатель затраченных
ресурсов (энергии, времени и т. д.).
- безразмерный показатель затраченных
ресурсов (энергии, времени и т. д.).
Коэффициент эффективности
показывает, насколько изменение стратегии поведения улучшает или ухудшает
достижение цели объекта. Коэффициент записан в обобщенном виде. Для каждой
конкретной системы коэффициент должен уточняться.
В качестве примера, для
системы управления комплексом лифтов, коэффициент эффективности выглядит
следующим образом:
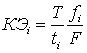 (2.6),
(2.6),
где 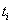 - время
прошедшее от момента вызова лифта пассажиром до прибытия лифта на этаж;
- время
прошедшее от момента вызова лифта пассажиром до прибытия лифта на этаж;
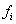 - количество этажей, пройденных
лифтом к пассажиру;
- количество этажей, пройденных
лифтом к пассажиру;
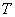 - максимально возможное время
прибытия лифта на этаж (время прибытия лифта на последний этаж, отправление с
первого, остановки на всех этажах);
- максимально возможное время
прибытия лифта на этаж (время прибытия лифта на последний этаж, отправление с
первого, остановки на всех этажах);
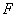 - максимально возможное количество
пройденных этажей (с первого по последний).
- максимально возможное количество
пройденных этажей (с первого по последний).
Коэффициентов эффективности
может быть несколько, в зависимости от сложности системы управления.
В ходе работы системы желательно
выполнения следующего условия:
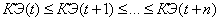 (2.7)
(2.7)
Таким образом, за счет
политики самообучения, должен обеспечиваться рост коэффициента эффективности во
время работы системы. Но алгоритм роста подкрепления не гарантирует.
Правила самообучения учителя
изменяют адаптационные параметры и сформулированы следующим образом:
·
если
снизилось значение коэффициента эффективности, то изменяем АП в противоположном
направлении от предыдущих изменений;
·
если
значение выросло, то продолжаем изменять АП в направлении от предыдущих
изменений;
·
если
значение не изменилось, то в зависимости от коэффициента эффективности либо
оставляем текущие правила (если коэффициент эффективности устраивает), либо
хаотически изменяем применяемое правило.
Шаг изменения АП нужно
уменьшать в зависимости от относительной величины изменения коэффициента
эффективности, чтобы не перешагнуть оптимум. Т.е. если коэффициент
эффективности изменился сильно, то и АП изменять сильно, если слабо, то и АП
слабо. При этом неважно вырос коэффициент эффективности или снизился.
Представим правила
изменения АП в виде продукций, в случае одного адаптационного параметра системы
и 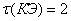 ,
, 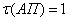 :
:
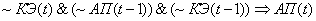 (2.8)
(2.8)
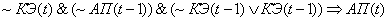 (2.9)
(2.9)
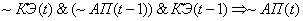 (2.10)
(2.10)
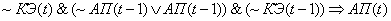 (2.11)
(2.11)
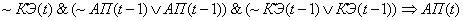 (2.12)
(2.12)
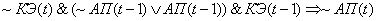 (2.13)
(2.13)
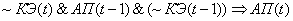 (2.14)
(2.14)
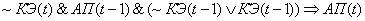 (2.15)
(2.15)
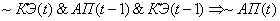 (2.16)
(2.16)
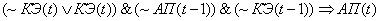 (2.17)
(2.17)
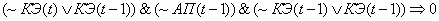 (2.18)
(2.18)
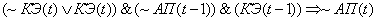 (2.19)
(2.19)
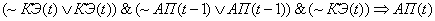 (2.20)
(2.20)
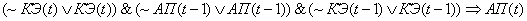 (2.21)
(2.21)
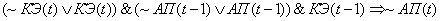 (2.22)
(2.22)
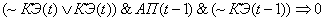 (2.23)
(2.23)
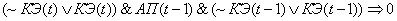 (2.24)
(2.24)
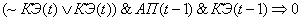 (2.25)
(2.25)
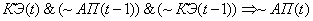 (2.26)
(2.26)
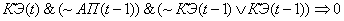 (2.27)
(2.27)
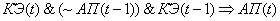 (2.28)
(2.28)
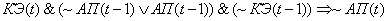 (2.29)
(2.29)
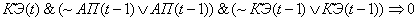 (2.30)
(2.30)
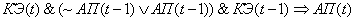 (2.31)
(2.31)
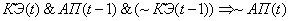 (2.32)
(2.32)
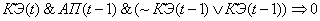 (2.33)
(2.33)
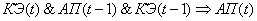 (2.34)
(2.34)
Поясним правила на
примере первого: если на текущем цикле управления коэффициент эффективности
снизился и в предыдущий цикл управления адаптационный параметр и коэффициент
эффективности снизились, то увеличиваем значение адаптационного параметра.
Формулы созданные по
данному принципу могут легко интерпретироваться для выборки нейросети учителя.
Действие системы определяется разницей между целевым и действительным
состоянием системы – чем больше разница, тем больше амплитуда изменения АП.
Также можно использовать
метод резолюций [73] для выработки новых правил на основании
первоначальных (например, формулы 2.8 – 2.34) и накопленной истории (рисунок
12).
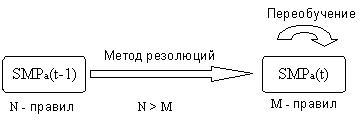
Рисунок 12
- Метод резолюций
В
случае использования принципа резолюций можно реализовать интересную схему
обучения самообучению, в которой изменяются не только правила управления, но и
количество правил самообучения (рисунок 13).
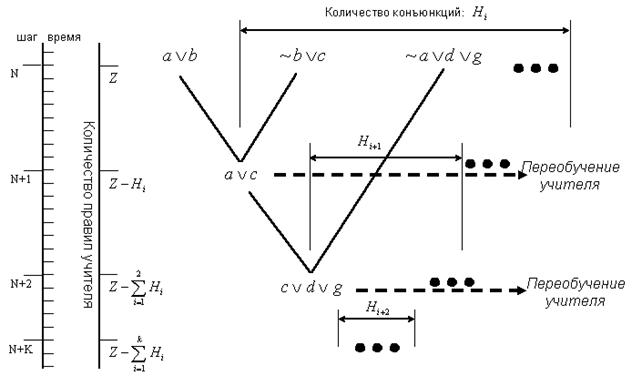
Рисунок 13 - Метод резолюций для изменения
правил учителя
На каждом шаге применения
резолюций, количество правил в базе учителя уменьшается и вычисляется по
формуле (2.35).
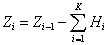 (2.35)
(2.35)
где 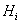 - количество резолюций на
- количество резолюций на 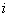 шаге;
шаге;
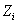 - количество правил на
- количество правил на 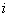 шаге.
шаге.
Следует отметить, что
переобучение учителя после каждого сокращения правил может занимать
значительное время.
Моторики
непосредственно управляют объектом. Управляющий сигнал с решателя поступает в моторики,
а затем подается на исполнительные средства. Моторики при этом занимаются
преобразованием сигнала решателя на «доступный» исполнительным устройствам
язык. Моторики могут реализовываться произвольным образом. В моториках
реализуются простейшие функциональные зависимости, такие как денормализация
сигнала и т.п.
2.2.7 Взаимодействие компонент
Взаимодействие компонент системы управления достаточно тривиально.
На каждом цикле управления происходит следующее (рисунок 14):
·
сенсоры вычисляют показатели для решателя и БКЭ;
·
решатель вычисляет управляющее воздействие
согласно текущим правилам управления;
·
БКЭ вычисляет КЭ на текущем цикле и динамику
изменения КЭ по сравнению с прошлыми циклами;
·
учитель получает
данные об изменении КЭ и применяет правила самообучения. На выходе
получаем измененные правила управления;
·
решатель дообучается (переобучается) по
измененным правилам;
·
моторика формирует управляющие воздействия на
исполнительные механизмы.
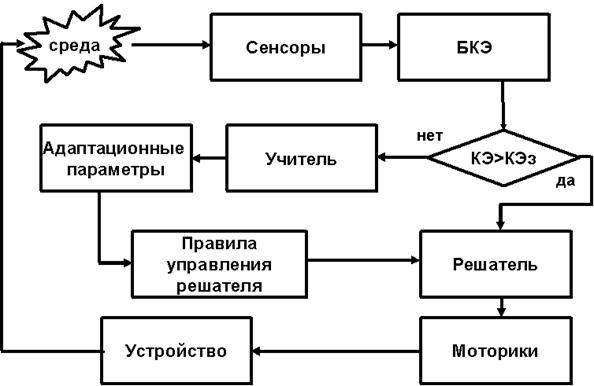
Рисунок 14 -
Алгоритм работы топологии «внутренний учитель»
Взаимодействие
правил учителя и решателя показано на рисунке 15.
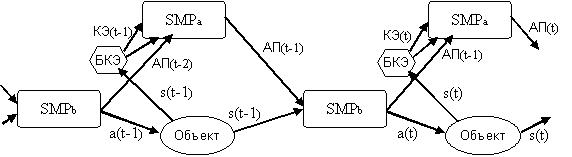
Рисунок 15 - Взаимодействие правил управления и самообучения
Строить обучение на
подобии обучения человека, принцип действия которого к настоящему моменту, к
сожалению, все еще остается загадкой, мы не будем. Были взяты только некоторые
подходящие моменты, которые можно реализовать доступными средствами.
Очень часто люди не
задумываются, почему они придерживаются той или иной точки зрения. Так сегодня
значительная часть исследователей и инженеров, занимающихся адаптивными
системами, априори придерживаются принципа «бытие определяет сознание», а,
следовательно, и действия. Такой взгляд на вещи, предполагает, что обучение
состоит в нахождении закономерностей в том потоке информации, который доступен
из наблюдения, поступает на вход системы. Естественно, при таком подходе модель
системы, обладающая адаптивным поведением, будет представлять собой некоторое
отображение множество входных данных на множества выходов, управляющих
поведением системы. При этом обучение, адаптивность поведения которого обычно
описывается детерминированными алгоритмами, изменяющими функцию отображения.
Использование таких принципов, позволяет быстро создавать приемлемые модели
адаптивных систем, которые обеспечивают достаточно гибкое поведение в среде, на
которую рассчитывал конструктор. Однако, при соприкосновении с неожиданными
изменениями среды, с необходимостью использования нестандартных ходов, такая
«отражательная» детерминированная схема
не работает.
Для работы топологии
«внутренний учитель» рассматривается общий вид процессов, как марковских, так и
немарковских. Это связанно с тем коэффициент эффективности, по сути, является
статистически накапливающемся, и с тем, чтобы для системы не было ограничений
по входной информации. В универсальности большую роль играет использование
аппарата нейросетей.
Планирование
подразумевает, что система должна не просто реагировать на текущие события, но
и прогнозировать последовательность действий или событий, которые должны
привести ее к намеченной цели.
В идеале система могла бы
строить модели внешнего мира, проводить "мысленные эксперименты" и
планировать действия в соответствии с результатами этих "экспериментов".
Но мы только отметим
возможность построения моделей внешнего мира в "сознании" системы.
Можно отметить модель мотивационного поведения MonaLysa (теория аниматов) [124,156].
В данной работе воплощена простая схемы планирования. В приведенной там схеме
планирования конечная цель действий разбивается на подцели, и система
"планирует" выполнение последовательности действий, каждое из которых
соответствует текущей ситуации и текущей подцели. При этом выполнение всей
последовательности приводит к достижению намеченной конечной цели.
Существуют ситуации,
когда системе необходимо подсказывать (наталкивать), что она должна делать. К
таким ситуациям относятся, например:
·
увеличение
уровня продаж в канун праздников;
·
увеличение
пассажиропотока на этаж при проведении на нем мероприятия (конференции);
Можно вводить расписание
применения правил самообучения или управления в необходимые циклы управления,
как показано на рисунке 16.
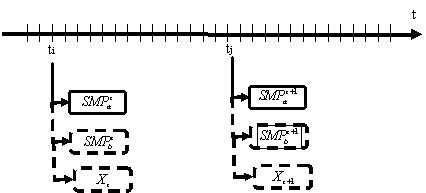
Рисунок 16 - Планирование
Взаимодействие компонент,
принимающих участие в управлении и самообучении, происходит следующим образом:
после старта, система работает по правилам управления 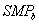 ,
которые заложены в нее разработчиком. Параметры адаптации и список правил «по
умолчанию» заложен в систему с самого начала.
,
которые заложены в нее разработчиком. Параметры адаптации и список правил «по
умолчанию» заложен в систему с самого начала.
Постепенно, система
накапливает информацию о коэффициенте эффективности, т.е. о качестве
управления. Компонента обратной связи, накапливая историю о коэффициенте
эффективности, начинает выдавать информацию учителю. Учитель получает динамику
изменения коэффициента эффективности.
Заложенные изначально в
систему правила рассчитаны на некоторый характер поведения среды. Пока характер
среды существенно не меняется, коэффициент эффективности, в среднем, также
остается неизменным. Учитель понимает, что корректировки правил управления не
требуется (тут имеется один нюанс, который мы рассмотрим ниже).
Если характер воздействия
среды изменился, и коэффициент эффективности существенно снизился, то учитель запускает
процесс самообучения. Учитель начинает изменять правила управления.
Подстраивать параметры адаптации, добавлять или удалять правила. После каждого
изменения, учитель останавливается и ждет обратной связи. Компонента обратной
связи выдают новую динамику коэффициента эффективности, учитывающую внесенные
изменения. Так реализуется метод проб и ошибок, - после попытки изменения, учитель
ждет результатов и анализирует их.
Если коэффициент
эффективности вырос, то учитель продолжает изменять параметры адаптации и
правила аналогичным образом.
Если коэффициент
эффективности снизился, то учитель меняет знак изменения параметров адаптации.
Этот цикл повторяется в
течении жизни системы.
Нюанс заключается в том,
что в случае, когда коэффициент эффективности довольно долго не изменяется, учитель
«встряхивает» параметры адаптации (если, конечно, нас не устраивает текущий
коэффициент эффективности). Т.е. произвольно изменяет параметры, независимо от
динамики коэффициента эффективности. Это необходимо для того, чтобы система
могла выйти из «мертвой зоны», - длительная неизменность коэффициента
эффективности может говорить о том, что управление оптимально, но, также, и о
том, что управление не оптимально, но неизменно.
При разработке прикладной
реализации необходимо проанализировать проблему и сформулировать правила самообучения.
Система должна адаптироваться к изменениям среды. Среда ведет себя
недетерминировано. Но, хотя присутствует недетерминированость, нужно выделить
такие классы воздействий среды, которые система будет отрабатывать. Невозможно
реализовать систему, которая отрабатывала бы вообще любые воздействия среды, но
те воздействия, которые критичны для системы и объекта в целом, необходимо
учитывать.
Если управляемый объект
имеет несколько адаптационных параметров то, оптимально управляя всеми при
любых воздействиях среды, можно говорить о том, что управление оптимально в
целом. Но управление такого рода, в общем случае, невозможно. Таким образом,
необходимо выделить такие адаптационные параметры объекта, которыми необходимо
управлять, для оптимального управления в таких классах воздействия среды, о
которых мы говорили ранее.
Таким образом,
первоначальная задача:
·
выделение
критичных для системы классов воздействия недетерминированной среды на объект;
·
выделение
адаптационных параметров объекта, которыми система будет адаптивно управлять,
реализуя задачу и отрабатывая воздействия среды.
После проведения
вышеописанных мероприятий у разработчика будет сформировано некоторое понятие о
характере среды, а также о том, как система будет адаптироваться к среде.
На следующем шаге,
необходимо сформулировать правила управления объектом без адаптации. Правила (продукции,
нечеткие правила и т.д.) будут описывать управление объектом решателем без
адаптации.
Следующим шагом будет
доработка правил управления:
·
необходимо
выделить компоненты правил управления, которые будут адаптивно подстраиваться
под среду;
·
необходимо
предусмотреть такое поведение решателя и предложенного набора правил, когда
некоторые правила добавляются или удаляются (т.е. при адаптации некоторые
правила могут появиться, а также исчезнуть).
Вышеперечисленное
необходимо для того, что сформулировать политику самообучения. Политика должна
заключаться в том, что недетерминированное воздействие среды влияет на сами
правила управления. При этом:
·
воздействие
среды, не носящее характер кардинальной новизны, должно отрабатываться
правилами управления без изменения их самих;
·
воздействие
среды, являющееся новым, неизвестным для системы управления, должно приводить к
корректировке набора правил управления (изменению, добавлению и удалению
правил);
Таким образом, на выходе
этого этапа разработки будем иметь сформулированные правила управления объектом
плюс способы их изменения. Следующим шагом разработаем правила самообучения.
Уже выделенные ранее характеры изменения среды, а также разработанные для их
отработки способы изменения правил требуют правил самообучения. На выходе правил
самообучения мы должны иметь параметры изменения правил управления. На входе –
динамика изменения коэффициента эффективности и адаптационных параметров.
Таким образом, получим
два набора правил – модифицируемые правила управления, а также правила самообучения.
Для того чтобы идеология
самообучения реализации была законченной, необходимо сформулировать коэффициент
эффективности. Как говорилось выше, а также в 1ой главе, подкрепление
(коэффициент эффективности) должно отражать основную цель системы, а также
количественные характеристики процесса деятельности системы. Таким образом,
становится очевидно, что в расчете коэффициента эффективности должны
присутствовать в числителе показатель того, достигнута ли цель или нет
(подкрепление рассчитывается на полном цикле управления), а в знаменателе
–затраты объекта управление на достижение цели. При больших затратах на
достижение цели, коэффициент эффективности уменьшается, так как система
отработала хуже.
Другой подход построения
идеологии самообучения заключается в выделении и расстановке приоритетов
параметров адаптации системы. Подход будет заключаться в том, что адаптируясь,
система будет подстраивать сначала работу с одним адаптационным параметром, а
уже затем со следующим и т.д. по порядку.
Таким образом, процесс
самообучения будет выглядеть следующим образом:
·
Адаптируем
управление одним адаптационным параметром, остальными управляем по изначально
вложенным правилам.
·
После
того, как коэффициент эффективности перестает расти, начинаем адаптировать
следующий адаптационный параметр по приоритетам.
Такой подход будет
логично отображать процесс самообучения для реальных объектов управления,
действующих в недетерминированной среде.
Пластичность нейронной
сети можно рассчитать, например, с помощью константы Липшица [37]. Рассмотрим послойно - полносвязную нейронную сеть
прямого распространения, а именно этот тип нейронных сетей использовался для
решателя и учителя в экспериментах, со следующими свойствами:
·
число
входных сигналов - 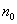 ;
;
·
число
нейронов в 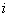 -м слое
-
-м слое
- 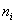 ;
;
·
каждый
нейрон первого слоя получает все входные сигналы, а каждый нейрон любого слоя
получает сигналы всех нейронов предыдущего слоя;
·
все
нейроны всех слоев имеют одинаковые характеристики;
·
все
синоптические веса ограничены по модулю единицей;
·
в
сети 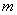 слоев.
слоев.
В этом случае константа
Липшица для 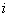 -го слоя
можно оценить следующей величиной:
-го слоя
можно оценить следующей величиной:
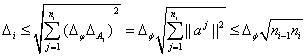 (2.36)
(2.36)
Оценка константы Липшица
всей сети:
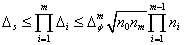 (2.37)
(2.37)
Если используется функция
активации гиперболический тангенс, то 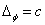 и оценка константы Липшица сети равна:
и оценка константы Липшица сети равна:
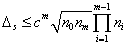 (2.38)
(2.38)
Если заменить всю область
определения функций D на конечное множество (задачник), то условие, определяющее требуемый
объем нейронной сети можно получить, сравнивая 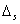 с оценкой константы Липшица для обучающей
выборки:
с оценкой константы Липшица для обучающей
выборки:
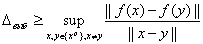 . (2.39)
. (2.39)
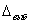 является нижней оценкой константы Липшица
аппроксимируемой функции. Нейросеть может реализовать данную функцию только в
том случае, когда
является нижней оценкой константы Липшица
аппроксимируемой функции. Нейросеть может реализовать данную функцию только в
том случае, когда 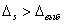 .
.
Также емкость сети можно
оценить следующим способом - для нейросетей с тремя слоями, то есть входным, выходным
и одним скрытым слоем, детерминистская емкость сети Cd оценивается так:
Nw/Ny<Cd<Nw/Ny×log(Nw/Ny) (2.40),
где Nw – число подстраиваемых
весов, Ny – число нейронов в выходном слое.
Следует отметить, что
данное выражение получено с учетом некоторых ограничений. Во-первых, число
входов Nx и нейронов в скрытом слое Nh должно удовлетворять неравенству
Nx+Nh>Ny. Во-вторых, Nw/Ny>1000. Однако вышеприведенная оценка
выполнялась для сетей с активационными функциями нейронов в виде порога, а
емкость сетей с гладкими активационными функциями, обычно больше. Кроме того,
фигурирующее в названии емкости прилагательное "детерминистский" означает,
что полученная оценка емкости подходит абсолютно для всех возможных входных
образов, которые могут быть представлены Nx входами. В действительности
распределение входных образов, как правило, обладает некоторой регулярностью,
что позволяет нейросети проводить обобщение и, таким образом, увеличивать
реальную емкость. Так как распределение образов, в общем случае, заранее не
известно, мы можем говорить о такой емкости только предположительно, но обычно
она раза в два превышает емкость детерминистскую.
Также в ходе
экспериментов выявлено, что все перепробованные способы определения количества
слоев и нейронов в них, по сути, являются лишь рекомендациями – реально же
нейронная сеть определялась следующим образом: выбор количества слоев и
нейронов по формулам и затем пакетный поиск лучшей нейросети, параметры
нейросетей в пакетах при этом различаются.
Универсальность
предложенной топологии подтверждается тем, что компоненты можно, в зависимости
от задачи, реализовывать различными способами, например, использовать нечеткую
логику в компоненте учитель.
Рассмотрим случай, когда
в системе один адаптационный параметр, 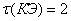 и
и 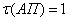 .
Пусть входными переменными будут:
.
Пусть входными переменными будут: 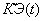 ,
, 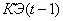 и
и 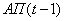 .
Выходной переменной будет
.
Выходной переменной будет 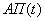 . Для
лингвистической оценки будем использовать 3 терма: снизился, остался, увеличился.
. Для
лингвистической оценки будем использовать 3 терма: снизился, остался, увеличился.
В системе типа Мамдани
используются правила следующего вида:
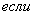
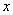
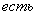
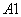
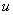
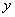
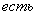
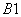 ,
, 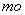
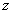
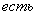
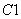
 (2.41)
(2.41)
Тогда правила
самообучения учителя (2.8 – 2.34) будут выглядеть следующим образом:
1. Если
Если 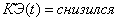 и
и 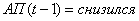 и
и 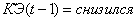 , то
, то 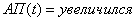 (2.42)
(2.42)
2. Если
Если 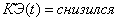 и
и 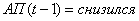 и
и 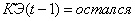 ,
то
,
то 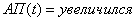 (2.43)
(2.43)
3. Если
Если 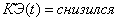 и
и 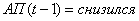 и
и 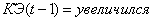 , то
, то 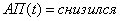 (2.44)
(2.44)
4. Если
Если 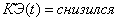 и
и 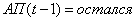 и
и 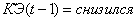 , то
, то 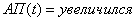 (2.45)
(2.45)
5. Если
Если 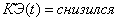 и
и 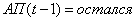 и
и 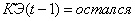 , то
, то 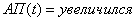 (2.46)
(2.46)
6. Если
Если 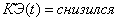 и
и 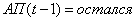 и
и 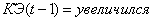 , то
, то 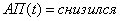 (2.47)
(2.47)
7. Если
Если 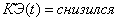 и
и 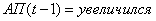 и
и 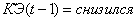 , то
, то 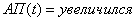 (2.48)
(2.48)
8. Если
Если 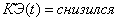 и
и 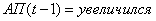 и
и 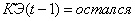 , то
, то 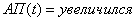 (2.49)
(2.49)
9. Если
Если 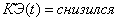 и
и 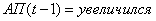 и
и 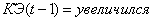 , то
, то 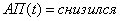 (2.50)
(2.50)
10. Если
Если 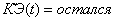 и
и 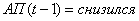 и
и 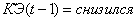 , то
, то 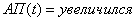 (2.51)
(2.51)
11. Если
Если 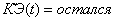 и
и 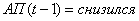 и
и 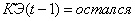 , то
, то 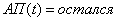 (2.52)
(2.52)
12. Если
Если 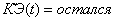 и
и 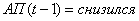 и
и 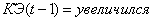 , то
, то 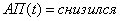 (2.53)
(2.53)
13. Если
Если 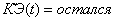 и
и 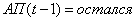 и
и 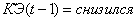 , то
, то 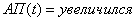 (2.54)
(2.54)
14. Если
Если 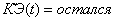 и
и 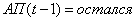 и
и 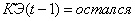 , то
, то 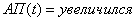 (2.55)
(2.55)
15. Если
Если 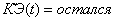 и
и 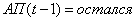 и
и 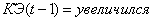 , то
, то 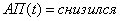 (2.56)
(2.56)
16. Если
Если 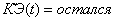 и
и 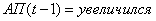 и
и 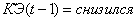 , то
, то 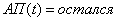 (2.57)
(2.57)
17. Если
Если 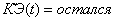 и
и 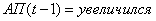 и
и 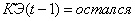 , то
, то 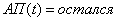 (2.58)
(2.58)
18. Если
Если 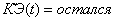 и
и 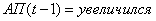 и
и 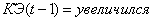 , то
, то 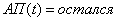 (2.59)
(2.59)
19. Если
Если 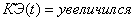 и
и 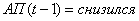 и
и 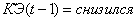 , то
, то 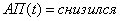 (2.60)
(2.60)
20. Если
Если 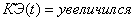 и
и 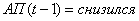 и
и 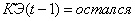 , то
, то 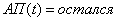 (2.61)
(2.61)
21. Если
Если 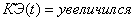 и
и 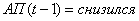 и
и 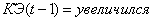 , то
, то 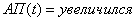 (2.62)
(2.62)
22. Если
Если 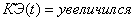 и
и 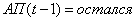 и
и 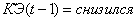 , то
, то 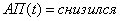 (2.63)
(2.63)
23. Если
Если 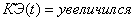 и
и 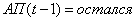 и
и 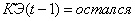 , то
, то 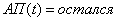 (2.64)
(2.64)
24. Если
Если 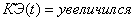 и
и 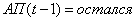 и
и 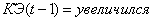 , то
, то 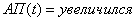 (2.65)
(2.65)
25. Если
Если 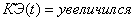 и
и 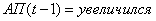 и
и 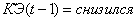 , то
, то 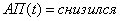 (2.66)
(2.66)
26. Если
Если 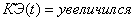 и
и 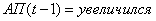 и
и 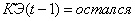 , то
, то 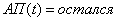 (2.67)
(2.67)
27. Если
Если 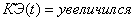 и
и 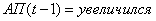 и
и 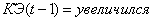 , то
, то 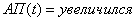 (2.68)
(2.68)
Правила самообучения
учителя можно представить графически, как показано на рисунке 17.
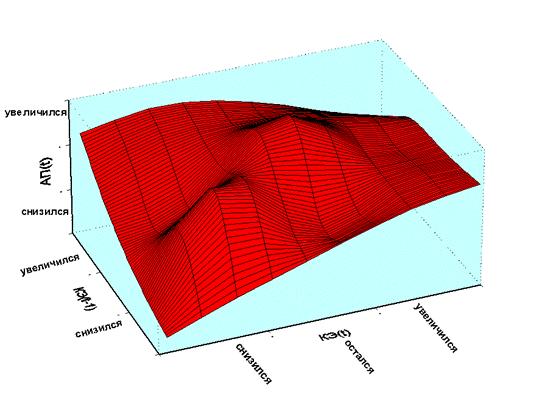
Рисунок 17 - Поверхность
правил учителя
Т. о. базу знаний
образуют нечеткие правила 2.42 – 2.68, при этом 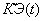 ,
, 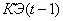 и
и 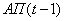 - имена входных переменных,
- имена входных переменных, 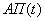 - имя переменной вывода. Далее алгоритм опишем
математически:
- имя переменной вывода. Далее алгоритм опишем
математически:
1. Нечеткость: находятся степени
истинности для предпосылок каждого правила: 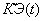 ,
, 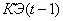 ,
, 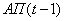 .
.
2. Нечеткий вывод: находятся уровни
отсечения для предпосылок каждого из правил (с использованием операции
минимума):
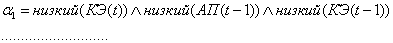 (2.69),
(2.69),
где через «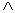 »
обозначена операция логического минимума. Затем находятся усеченные функции
принадлежности:
»
обозначена операция логического минимума. Затем находятся усеченные функции
принадлежности:
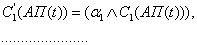 (2.70)
(2.70)
3. Композиция: с использованием операции
max (обозначено,
как «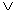 »)
производится объединение найденных усеченных функций, что приводит к получению
итогового нечеткого подмножества для переменной вывода с функцией
принадлежности:
»)
производится объединение найденных усеченных функций, что приводит к получению
итогового нечеткого подмножества для переменной вывода с функцией
принадлежности:
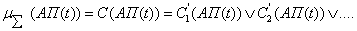 (2.71)
(2.71)
4. Приведение к четкости можно
производит, например, центроидным методом.
С помощью системы типа
Сугэно можно реализовать правила самообучения, которые изменяют параметры самых
правил. Сразу отметим, что система типа Сугэно трудна как при проектировании,
так и в реализации. В данном случае базу знаний образуют правила следующего
вида:

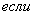
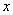
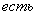
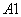
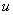
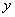
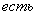
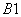 ,
, 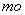
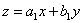 (2.72)
(2.72)
1. Первый этап – как в алгоритме
Мамдани.
2. На втором этапе находятся
уровни отсечения для предпосылок каждого правила – как в алгоритме Мамдани и
индивидуальные выходы правил по формулам:
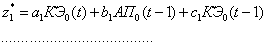 (2.73)
(2.73)
3. На третьем этапе определяется
четкое значение переменной вывода:
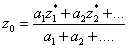 (2.74),
(2.74),
где 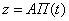 . В данном алгоритме необходимо подбирать коэффициенты
. В данном алгоритме необходимо подбирать коэффициенты 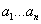 и
и 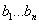 , что
является трудной задачей, но в тоже время изменение этих параметров (изменение
поверхности правил учителя) в процессе работы объекта, управляемого с помощью
топологии «внутренний учитель», значительно повышает адаптационные свойства
объекта, что является несомненным преимуществом использования модели Сугэно над
моделью Мадмани.
, что
является трудной задачей, но в тоже время изменение этих параметров (изменение
поверхности правил учителя) в процессе работы объекта, управляемого с помощью
топологии «внутренний учитель», значительно повышает адаптационные свойства
объекта, что является несомненным преимуществом использования модели Сугэно над
моделью Мадмани.