Лекция 6

 

 

Существуют разновидности нейронных сетей в которых присутствуют обратные связи. В частности такими сетями является нейросетевые архитектуры Хопфилда и Хемминга. В таких сетях веса синаптических связей рассчитываются в начале работы и больше не изменяются. С одной стороны у таких сетей есть большие ограничения по количеству запоминаемых образцов, с другой стороны такой подход значительно облегчает работу специалиста в некоторых задачах.

 

Сеть Хопфилда

Структурная схема сети Хопфилда представлена на рисунке. Сеть состоит из единственного слоя нейронов, число которых одновременно равно количеству входов и количеству выходов. Каждый нейрон связан синапсами остальными нейронами и имеет один вход. Выходные сигналы формируются как обычно на аксонах.

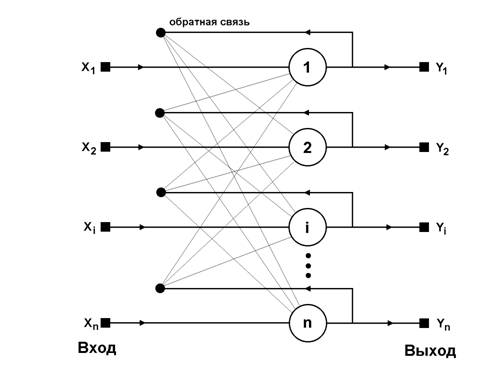
Рисунок 1. Сеть Хопфилда

Задача ассоциативной памяти, решаемая с помощью данной сети, обычно выглядит следующим образом – есть некоторый набор двоичных сигналов, которые считаются эталонными. Сеть должна уметь из произвольного входного сигнала выделить тот эталонный образец, который наиболее похож на поданный сигнал или же выдать сообщение о том, что поданный сигнал ни с чем не ассоциируется. Входной сигнал, в общем случае, может быть описан вектором 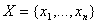.  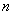- число нейронов в сети и размерность входных и выходных векторов. Каждый элемент вектора равен либо +1, либо -1.

При инициализации сети коэффициенты устанавливаются следующим образом:

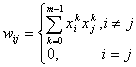
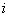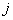 и  - коэффициенты предсинаптического и постсинаптического нейронов. x_i^k, x_j^k – i-ый и j-ый элементы вектора k-ого образца.

Алгоритм работы сети следующий:

1. На входы сети подается неизвестный сигнал. Практически его ввод происходит за счет установления аксонов y_i(0) = x_i , i = 0...n-1. То есть входы нужны лишь формально.
2. Рассчитывается новое состояние нейронов:

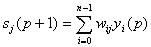, j=0...n-1

и новое состояние аксонов

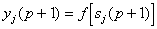
При этом 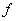 - функция единичного скачка.

3. Проверяется – изменились ли состояния аксонов за последнюю итерацию. Если да, то переход на пункт 2, если нет, то работа сети завершилась. На выходе получается эталонный образец наиболее похожий на входной вектор.

Отметим, что иногда сеть не может сопоставить эталонный образец и входной сигнал, при этом на выходе получается произвольный сигнал. Это связано с ограниченностью сети – сеть Хопфилда может запомнить не более 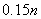 образцов. Также – если эталонные образцы 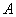 и 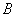похожи, то обычно происходят перекрестные ассоциации.

 

Сеть Хемминга

Если в задаче ассоциативной памяти нет необходимости в том, чтобы нейросеть выдавала эталонный образец, а достаточно только номера образца, то для этих целей используется сеть Хемминга. Структурная схема сети Хемминга представлена на рисунке 2.

 

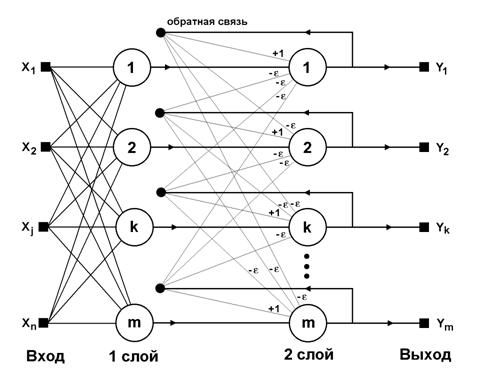
Рисунок 2. Сеть Хемминга

 

Данная сеть, в сравнении с сетью Хопфилда, характеризуется меньшими вычислительными затратами. В сети Хемминга два слоя – первый и второй слои состоят из 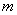 нейронов и  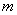равно числу образцов. Нейроны первого слоя имеют по 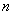 входных синапсов, где  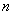- размерность входных векторов. Нейроны второго слоя связаны между собой обратными, отрицательными связями. Обратная связь от аксона на владельца нейрона равен +1. Суть работы состоит в нахождении расстояния Хемминга от тестируемого образца до всех образцов. Расстоянием Хемминга называется число отличающихся битов в двух бинарных векторах.

  - расстояние Хемминга равно 0.

 

 - расстояние Хемминга равно 2.

Сеть должна выбрать образец с минимальным расстоянием Хемминга до поданного входного сигнала – в результате активируется один выход, отвечающий за данный эталонный образец.

При инициализации сети весовым коэффициентам первого слоя и порогу активационной функции присваиваются следующие значения:

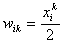, i=0...n-1, k=0...m-1

T_k = n / 2, k = 0...m-1

где x_i^k – i-ый элемент k-ого образца.

Весовые коэффициенты тормозящих синапсов во втором слое берут равными некоторой величине 0 < e < 1/m. Синапс нейрона, связанный с его же аксоном имеет вес +1.

Алгоритм работы сети Хэмминга следующий:

1. На входы сети подается неизвестный вектор X = {x_i:i=0...n-1}, исходя из которого рассчитываются состояния нейронов первого слоя (верхний индекс в скобках указывает номер слоя):

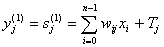, j=0...m-1                                                                         

После этого полученными значениями инициализируются значения аксонов второго слоя:

y_j⁽²⁾ = y_j⁽¹⁾, j = 0...m-1                                                                                                

2. Вычислить новые состояния нейронов второго слоя:

                                               

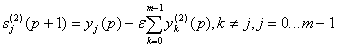
и значения их аксонов:

                                                                  

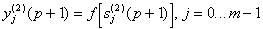
Активационная функция f имеет вид порога, причем величина F должна быть достаточно большой, чтобы любые возможные значения аргумента не приводили к насыщению.

3. Проверить, изменились ли выходы нейронов второго слоя за последнюю итерацию. Если да – перейди к шагу 2. Иначе – завершение работы.

Из оценки алгоритма видно, что роль первого слоя нейронов весьма условна: воспользовавшись один раз на шаге 1 значениями его весовых коэффициентов, сеть больше не обращается к нему, поэтому первый слой может быть вообще исключен из сети (просто заменен на матрицу весовых коэффициентов.