Лекция 3

 

Парадигмы обучения нейронных сетей. Алгоритм решения задач с помощью нейронных сетей. Алгоритм обратного распространения ошибки. Расписание обучения нейронных сетей.

 

Парадигмы обучения нейронных сетей

Существует две парадигмы обучения нейронных сетей – с учителем и без учителя. В первом случае, на входной вектор имеется готовый ответ, во втором случае нейронная сеть самообучается. У каждого вида обучения есть своя ниша задач и по большому счету они не пересекаются. На данный момент придумано и запатентовано большое количество архитектур нейронных сетей и методов их обучения. Но основными (исходными) являются – для обучения с учителем это «алгоритм обратного распространения ошибки», а для обучения без учителя это алгоритмы Хебба и Кохонена. Эти парадигмы сильно пересекаются с биологической действительностью, например – ребенок обучается с учителем или без? Правильным, я думаю считать, что и так и так, что – то показывают родители или учителя, чему – то ребенок обучается сам. В тоже время есть, как – бы половинчатые примеры обучения – езда на велосипеде, ребенок видит, как это происходит у других, но сам процесс обучения по сути, он проходит самостоятельно – падая и начиная сначала. Также, в последнее время, сформировалась новая, третья парадигма – обучение с подкреплением, но о ней поговорим ниже. Отметим в данный момент только, что в этой парадигме есть и обучение с учителем и обучение без учителя.

 

Алгоритм решения задач с помощью нейронных сетей

Для решения задач с помощью нейросетей необходимо:

·        Рассмотреть поставленную задачу и подумать, а не проще ли ее решить с помощью других методов.

·        Определиться с начальным пулом значащих входов. Пул входов обычно перебирается в течение времени и выбираются те, на которых дается наименьшая ошибка.

·        Выбрать, что будет на выходе нейронной сети, то есть определить выходные переменные.

·        Определиться с начальным количеством слоев и нейронов в них (опять же количество слоев и нейронов в них обычно перебирается в течении обучения).

·        Сгенерировать сеть и обучить ее на заданных примерах.

 

Алгоритм обратного распространения ошибки

В этом алгоритме происходит распространение ошибки от выходов НС ко входам, то есть в направлении обратном распространению сигналов обычном режиме работы. Согласно методу наименьших квадратов, минимизируемой целевой функцией ошибки НС является величина:

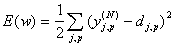
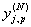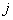где  реальное выходное состояние нейрона  выходного слоя N нейронной сети при подаче на ее входы 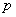 - го образа;  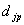- желаемое (идеальное) выходное состояние этого нейрона. Суммирование происходит по всем нейронам выходного слоя и по всем обрабатываемым сетью образам[1]. Минимизация ведется методом градиентного спуска, что означает подстройку весовых коэффициентов следующим образом:

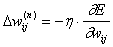
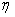 - коэффициент скорости обучения, .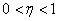

Обучение методом обратного распространения ошибки происходит в соответствии со следующими пунктами:

1. Подать на входы НС образец выбранный случайным образом и в режиме обычного функционирования НС рассчитать ее выходы.

2. Рассчитать дельту ошибки для выходного слоя по формуле:

[2]

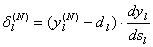
3. Рассчитать изменения весов для выходного слоя N по формуле:

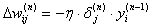         (3)

4. Рассчитать ошибки и изменения весов (формула 3) для всех остальных слоев по формулам:

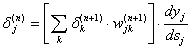
5. Скоректировать все веса нейронной сети по формуле:

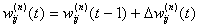
6. Если ошибка сети существенна, то перейти на на шаг 1. В противном случае – конец обучения.

Изменение весов нейронной сети можно вести также с помощью формулы:

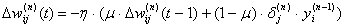
где 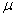 - коэффициент инерционности. Эта формула позволяет «гладко» изменять веса, что приводит к понижению перепадов ошибки. Формулу () целесообразно применять в конце обучения, когда ошибка близка к заданной.

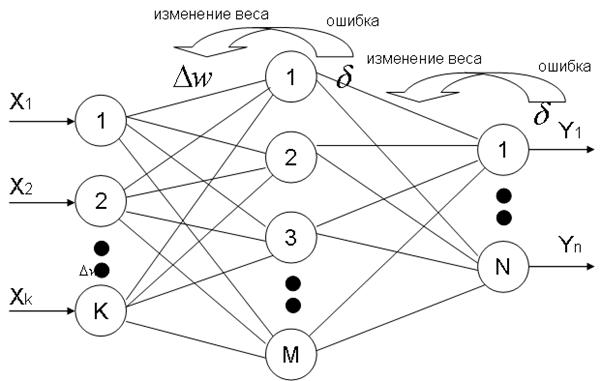
Рисунок 1. Пояснение алгоритма обратного распространения ошибки

 

 

Расписание обучения

Веса и пороговые уровни инициализируются случайными значениями. Созданная таким образом сеть абсолютно неадекватна решаемой задаче и может генерировать на выходе только шум. Поэтому ошибка в начале обучения очень велика, и есть смысл вводить большие коррекции параметров. Ближе к концу обучения ошибка значительно снижается, и коррекции должны быть малыми. Чтобы менять длину шагов по параметрам, используют расписание обучения (learning schedule). Выберем скорость обучения зависящей от времени обучения: ( ) t ε . Обычно скорость монотонно убывает с ростом времени. Для сходимости алгоритма необходимо:

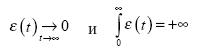
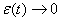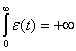Часто выбирают и  или аналогичные функции.

Алгоритмы с расписанием обучения сходятся быстрее, т.к. в начале используются большие коррекции, и дают более точные результаты за счет точной настройки параметров в конце обучения. Уменьшение шагов к концу алгоритма сходно с методом имитации отжига, который рассматривается далее. Сходство проявляется еще и в том, что преодолеваются локальные минимумы на начальном этапе обучения. Коррекции настолько велики, что параметры "проскакивают" оптимальное значение и сеть попадает в область притяжения другого минимума, а не задерживается в первом найденном минимуме.