Лекция 2
Персептрон
Рассмотрим
формальный нейрон – простейший элемент теории нейронных сетей. По структуре и
принципу работы – это, по сути Персептрон Розенблатта, первой нейросетевой
архитектуры.
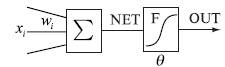
Рис. Формальный
нейрон.
Нейрон состоит из взвешенного сумматора и нелинейного элемента. Функционирование
нейрона определяется формулами:
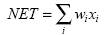
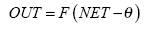
Где 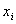 - входные сигналы,
совокупность которых формируют вектор
- входные сигналы,
совокупность которых формируют вектор 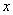 ;
;
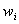 - весовые коэффициенты,
совокупность которых образуют вектор весов
- весовые коэффициенты,
совокупность которых образуют вектор весов 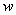 ;
;
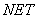 - взвешенная сумма
входных сигналов, значение
- взвешенная сумма
входных сигналов, значение 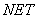 передается на нелинейный элемент;
передается на нелинейный элемент;
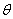 - пороговый уровень
данного нейрона;
- пороговый уровень
данного нейрона;
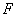 - нелинейная функция,
называемая функцией активации.
- нелинейная функция,
называемая функцией активации.
Нейрон имеет
несколько входных сигналов 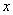 и один выходной сигнал
и один выходной сигнал 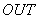 .
.
Виды функций активации
Рассмотрим наиболее
распространненые функции активации  .
.
- Жесткая ступенька
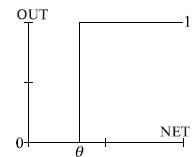
Работа описывается следующей
формулой:
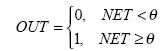
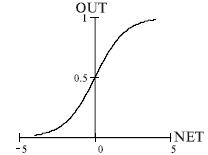
- Сигмоида (функция Ферми)
Функция описывающая сигмоиду:
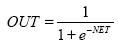
Часто
применяются для многослойных перцептронов и других сетей с непрерывными
сигналами. Гладкость, непрерывность функции — важные положительные качества.
Непрерывность первой производной позволяет обучать сеть градиентными методами
(например, метод обратного распространения ошибки).
Функция
симметрична относительно точки (NET=0, OUT=1/2), это делает равноправными
значения OUT=0 и OUT=1, что существенно в работе сети. Тем не менее, диапазон
выходных значенийот 0 до 1 несимметричен, из - за этого обучение значительно
замедляется. Значение производной выражается через саму функцию, что приводит к
увеличению скорости расчета производной при обучении сети (см. ниже).
- Гиперболический тангенс
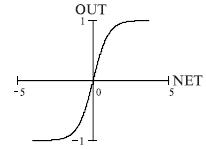
Функция:
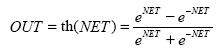
Также часто применяется в сетях с непрерывными сигналами. Производная
выражается через саму функцию.
- SOFTMAX – функция
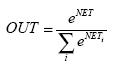
В данном случае суммирование ведется по всем нейронам данного слоя
сети. Такой выбор обеспечивает сумму выходов слоя, равную единице при любых
значениях сигнала  данного
слоя. Это позволяет трактовать выход
данного
слоя. Это позволяет трактовать выход  как вероятность событий, совокупность
которых образует полную группу.
как вероятность событий, совокупность
которых образует полную группу.
Выбор функции активации выбирается в зависимости от задачи, удобством
программной (аппартной) реализации, а также алгоритмом обучения.
Ограничения модели нейрона
В теории
нейронных сетей считается, что:
- Вычисления нейрона происходят
мгновенно, не внося задержку.
- Нет четких алгоритмов для
выбора функции активации.
- Нет механизмов регулирующих
работу сети в целом, на подобии гормональной регуляции активности в
нервных клетках.
- Модель формального нейрона не является
биоподобной и это скорее математическая абстракция.
Многослойный персептрон
Формальные нейроны могут
объединяться в сети различными способами. Рассмотрим простейшее объединение –
многослойный персептрон.
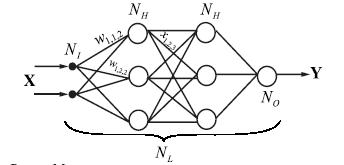
Сеть состоит из произвольного
числа слоев. Различают входной слой – на который поступает вектор 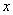 (обычно он не
учитывается в подсчете слоев), выходного слоя, который выдает результат
расчетов сети и скрытых слоев. Входной слой не выполняет никаких вычислений –
он просто распределяет вектор
(обычно он не
учитывается в подсчете слоев), выходного слоя, который выдает результат
расчетов сети и скрытых слоев. Входной слой не выполняет никаких вычислений –
он просто распределяет вектор 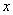 на следующий слой и служит приемником
информации. Обычно, если скрытых слоев больше, чем два, то во всех скрытых
слоях одинаковое количество нейронов.
на следующий слой и служит приемником
информации. Обычно, если скрытых слоев больше, чем два, то во всех скрытых
слоях одинаковое количество нейронов.
Работа многослойного персептрона
описывается следующими формулами:
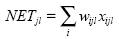
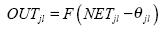
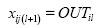
где индексом 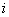 обозначим номер входа,
обозначим номер входа, 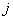 - номер нейрона в слое,
- номер нейрона в слое,
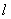 - номер слоя.
- номер слоя.
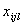 -
- 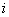 -й входной сигнал
-й входной сигнал 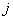 -го нейрона в слое
-го нейрона в слое 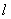 ;
;
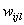 - весовой коэффициент
- весовой коэффициент 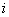 - го входа нейрона номер
- го входа нейрона номер 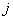 слоя
слоя 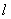 ;
;
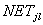 - сигнал NET нейрона номер
- сигнал NET нейрона номер 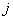 слоя
слоя 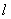 ;
;
И так далее..
Введем
обозначения: 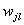 —
вектор-столбец весов для всех входов нейрона j в слое i.
—
вектор-столбец весов для всех входов нейрона j в слое i.
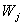 — матрица весов
всех нейронов в слоя j. В столбцах матрицы расположены
вектора
— матрица весов
всех нейронов в слоя j. В столбцах матрицы расположены
вектора 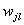 .
Аналогично
.
Аналогично 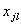 —
входной вектор-столбец слоя l.
—
входной вектор-столбец слоя l.
Каждый слой
рассчитывает нелинейное преобразование от линейной комбинации сигналов
предыдущего слоя. Многослойная нейронная сеть может формировать на выходе
произвольную многомерную функцию при соотвествующем выборе количества слоев,
диапазона изменения сигналов и параметров нейронов. Многослойные нейронные сети
являются универсальным аппроксиматором функций. Общая формула описывающая многослойный
персептрон:
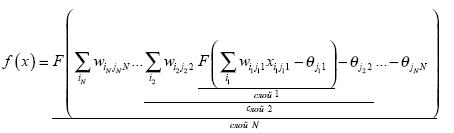
За счет поочередного
расчета линейных комбинаций и нелинейных преобразований достигается
аппроксимация произвольной многомерной функции при соотвествующем выборе
параметров сети.
<< Предыдущая лекция || Следующая лекция >>
Лекция 1. Основы нейросетей. Биологические нейронные сети.
Лекция 2. Персептрон. Многослойный персептрон.
Лекция 3. Алгоритм обратного распространения ошибки.
Лекция 4. Ускорение обучения. Обучение без учителя
Лекция 5. Сеть Кохонена. Звезды Гроссберга
Лекция 6. Сети Хопфилда и Хемминга
Лекция 7. Генетические алгоритмы
Лекция 8. Обучение с подкреплением
Лекция 9. Прогнозирование с помощью нейронных сетей
Лекция 10. Самообучаемые системы с самомодифицирующимися правилами
Нейросетевая топология Внутренний учитель