Лекция 4. Ускорение обучения нейросети. RPROP. Обучение без учителя

Как и любой градиентный алгоритм, метод обратного распространения "застревает" в локальных минимумах функции ошибки, т.к. градиент вблизи локального минимума стремится к нулю. Шаг в алгоритме обратного распространения выбирается неоптимально. Точный одномерный поиск дает

более высокую скорость сходимости. Возникает интересное явление, которое оправдывает неоптимальный выбор шага. Поверхность функции E(P) имеет множество долин, седел и локальных минимумов. Поэтому первый найденный минимум редко имеет малую величину E, и чем больше нейронов и синапсов в сети, тем меньше вероятность сразу найти глубокий минимум целевой функции. Если же шаг выбирается не оптимально, то он может оказаться достаточно большим, чтобы выйти из окрестности данного локального минимума и попасть в область притяжения соседнего минимума, который может оказаться глубже. Благодаря этому алгоритм способен находить более глубокие минимумы целевой функции, что повышает качество обучения. Есть другой способ преодоления локальных минимумов — обучение с шумом. Будем выбирать коррекцию для весов в виде:

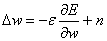
где n — случайная величина, имеющая нулевое математическое ожидание и небольшую дисперсию. Часто используется гауссовское распределение для n. Казалось бы, добавление шума должно снижать точность обучения. Так и происходит, скорость сходимости к данному локальному минимуму (если он единственный) снижается. Но если поверхность E(P) сложная, то шум помогает "вырваться" из данного локального минимума (выход из минимума тем вероятнее, чем меньше размеры его области притяжения), и найти более глубокий, возможно — глобальный минимум. Обучение с шумом снижает вероятность остановки алгоритма в неглубоком локальном минимуме

целевой функции.

Выбор длины шага обучения

Расчет длины шага обучения через градиент ошибки очень затратное дело. Поэтому обычно длину шага берут равной константе и либо оставляют в течении времени, либо пропорционально меняют в ходе обучения. При этом неудачный выбор шага приводит к:

1) к неточности обучения: оказавшись в окрестности локального минимума, когда требуются малые длины шага для точной настройки параметров, алгоритм с большим шагом даст неточные значения параметров;

2) к медленному обучению: если шаг слишком малый, обучение может стать недопустимо медленным;

3) к отсутствию сходимости, параличу сети и другим проблемам при очень большой длине шага.

Динамическое добавление нейронов

Адекватный выбор количества нейронов и слоев — серьезная и нерешенная проблема для нейронных сетей. Основным способом выбора остается прямой перебор различного количества слоев и определение лучшего. Для этого требуется каждый раз по новому создавать сеть. Информация, накопленная в предыдущих сеансах обучения, теряется полностью. Начинать перебор количества нейронов можно как с заведомо избыточного, так и с недостаточного. Независимо от этого, новая созданная сеть с другим количеством нейронов требует полного переобучения.

Динамическое добавление нейронов состоит во включении нейронов в действующую сеть без утраты ее параметров и частично сохраняет результаты, полученные в предыдущем обучении. Сеть начинает обучение с количеством нейронов, заведомо недостаточным для решения задачи. Для обучения используются обычные методы. Обучение происходит до тех пор, пока ошибка не перестанет убывать и не выполнится условие:

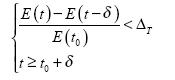
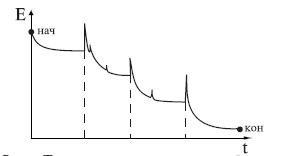
где t — время обучения; 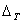— пороговое значение убыли ошибки; 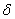— минимальный интервал времени обучения между добавлениями новых нейронов; t0 — момент последнего добавления; Когда выполняются оба условия, добавляется новый нейрон. Веса и порог нейрона инициализируются небольшими случайными числами. Обучение снова повторяется до тех пор, пока не будут

выполнены условия (). Типичная зависимость ошибки от времени обучения приведена на рис. . Моменты добавления новых нейронов отмечены пунктиром. После каждого добавления ошибка сначала резко возрастает, т.к. параметры нейрона случайны, а затем быстро сходится к меньшему значению.

Алгоритм RProp

Рассмотрим модификацию алгоритма обратного распространения ошибки – алгоритм Rprop (Resilent Propogation – «упругое распространение»). В этом алгоритме устранен основной недостаток BackProp - скорость обучения. Rprop использует знаки частных производных для подстройки весовых коэффициентов. Для определения величины коррекции используется следующее правило:

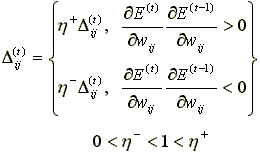
где

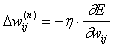
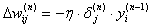
Если на текущем шаге частная производная по соответсвующему весу 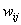изменила знак, то из этого следует, что последнее изменение было большим и алгоритм проскочил локальный минимум. Следовательно, величину изменения необходимо уменьшить на 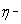и вернуть предыдущее значение весового коэффициента, то есть сделать «откат».

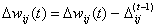
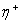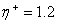Если знак частной производной не изменился, то нужно увеличить величину коррекции на для достижения более быстрой сходимости. Рекомендованные значения и 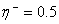, но нет никаких ограничений на использование других значений этих параметров. Начальные значения для всех 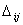обычно устанавливаются равными 0.1. Для вычисления значения коррекции весов используется следующее правило:

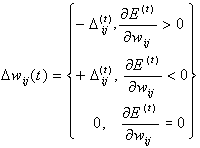
Если производная положительна, т. е. ошибка возрастает, то весовой коэффициент уменьшается на величину коррекции, в противном случае – увеличивается.

Затем подстраиваются веса:

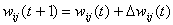
Суммируя вышенаписанное получаем следующий алгоритм:

1. Проинициализировать величину коррекции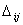

2. Предъявить все примеры из выборки и вычислить частные производные.

3. Подсчитать новое значение 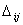по формулам 1 и 3.

4. Скорректировать веса по формуле 4.

5. Если условие останова не выполнено, то перейти к 2.

Данный алгоритм сходится в 4-5 раз быстрее, чем стандартный алгоритм Backprop.

Обучение без учителя. Алгоритм Хебба

Рассмотрим обучение нейронных сетей без учителя. В рассмотренных выше алгоритмах и примерах есть и входные значения и ответы, которые нейронная сеть должна воспроизвести. Но существует широкий пласт задач, в которых ответы заранее не известны, например, в задачах многомерной классификации. Обучение без учителя – «самостоятельно», здесь можно провести аналогию с обучением ребенка – что-то он познает с помощью учителя, чему – то учится на собственном опыте. Процесс обучения без учителя строится на том же принципе, что и обучение с учителем – подстраивании синаптических весов. Очевидно, что подстройка синапсов может происходить только на основании информации, доступной в нейроне, то есть его состояния и уже имеющихся весовых коэффициентов. Рассмотрим сигнальный метод обучения Хебба.

Веса по данному методу изменяются исходя из формулы:

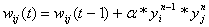
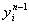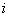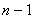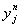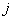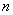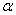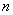где - выходное значение нейрона слоя , - выходное значение -го нейрона слоя . - коэффициент скорости обучения. - здесь и далее, номер слоя сети. При обучении данным методом усиливаются связи между возбужденными нейронами, что видно из второго слагаемого формулы.

Также есть и диффернциальный метод обучения Хеба.

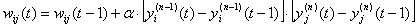
Как видно из формулы сильнее всего обучаются те синапсы, которые наиболее динамично изменились в сторону увеличения.

Полный алгоритм обучения методами Хебба выглядит следующим образом:

1. При инициализации сети всем весовым коэффициентам присваиваются небольшие случайные значения.

2. На входы подается выбранный случайным образом образ и сигналы возбуждения распространяются по всем слоям согласно принципам прямопоточных сетей.

3. На основании полученных выходных значений нейронов по формулам (1) или (2) происходит коррекция весовых коэффициентов.

4. Цикл с шага 2, пока выходные значения сети не застабилизируются с заданной точностью.

Отметим, что ид откликов на каждый класс входных образов заранее не известен и будет представлять собой произвольное сочетание состояний нейронов выходного слоя, обусловленное случайным распределением весов на стадии инициализации. При этом сеть способна обобщать схожие образцы, относя их к одному классу.

<< Предыдущая лекция || Следующая лекция >>

Лекция 1. Основы нейросетей. Биологические нейронные сети.
Лекция 2. Персептрон. Многослойный персептрон.
Лекция 3. Алгоритм обратного распространения ошибки.
Лекция 4. Ускорение обучения. Обучение без учителя
Лекция 5. Сеть Кохонена. Звезды Гроссберга
Лекция 6. Сети Хопфилда и Хемминга
Лекция 7. Генетические алгоритмы
Лекция 8. Обучение с подкреплением
Лекция 9. Прогнозирование с помощью нейронных сетей
Лекция 10. Самообучаемые системы с самомодифицирующимися правилами
Нейросетевая топология Внутренний учитель